The Secrets of Haboob Rendering

A study into the practicalities of ray marching the haboob

Wait 'Haboob' rendering? What is a haboob? Why should we render it?

The haboob is a classification of dust storm within meteorological circles. It consists of a large, rolling cloud of mineral dust that has been swept up from the ground by a spreading cool pool of air. This cool pool is typically formed from an overhead thundercloud, where precipitation creates a cool column of air that strikes the ground and sets the event in motion. It is surprising then that this atmospheric event is closely associated with arid regions - notably Sudan and the Sahara.

Not just Saharan dust.

There is a growing movement to classify the dust storms on Mars as haboobs. This implies the effect is more broad, fitting an inter-planetary context; and was the key inspiration behind this graphical research. Existing literature on atmospheric phenomena predominantly targets common effects like clouds and fog. Between these effects, there exists a general rendering solution for real-time volumetrics. However, atmospheric dust remains a footnote - assumed to fit the same umbrella without any formal study.

What makes dust so unique?

Several physical properties of dust (within the haboob context) were of interest to this study. Unlike clouds and fog which are generally uniform absorbers (i.e. a greyscale colouration), composition of the dust contains iron oxides which characteristically form a red-yellow colour spectra. Suspension of dust particles is part due to convectional current and part due to a process called saltation. This is where heavier dust particles are dragged along the ground, causing an electrostatic effect that repels smaller particles. The outcome is a vertical distribution of dust. The distribution of particle size has a correlation towards scattering spectrum, loosely related by an indicative value - the Ångström exponent. Both features imply dust exhibits a more complex, wavelength-dependent mode of rendering. Dust is also a greater absorber of irradiance than other effects...

Modern computer graphics attempts to represent atmospheric effects as 3D volumes.

Gone are the days of particle systems - the real deal is volumetric rendering. This is analogous to raytracing, however volumetric rendering is existentially more complicated and the associated computations are unnatural for GPU hardware. Assuming there is VRAM to spare, volumetric rendering consists of many texture samples spanning 3D space that describe pointwise optical properties. To simulate light through a volume, individual rays are projected from the camera and iteratively stepped along discrete distances to sample and numerically approximate interaction through said volume. The main bottleneck for this Monte Carlo algorithm is the number of samples - as compute groups have to wait for texture access. Due to the Nyquist limit, however, there must be twice the number of samples as the frequency of volumetric data for a good numerical match.

In reality, representing the contributions of light through a volume is an explosive problem. For every point along a ray, there exists other rays which scattered from that point on the unit sphere. This is a probabilistic process that cannot be represented in real-time - typically classified as multiple scattering. Offline path tracers will attempt to approximate this process via stochastic methods and importance sampling.

Fake it to make it!

The typical real-time volumetric tracer will assume lighting to be a two step process. Transmission along the ray and a single phase scattering contribution incoming to the ray. It was discovered that the typical functions - Beer-Lambert and Henyey-Greenstein respectively are indeed adequate for the haboob context. Within mereological literature, both functions are used to model the haboob - matching the existing graphical research on clouds and fog. However, there are two alterations that were made. Transmission is a product sampling problem.

The standard model appears to utilise a type of trapezium rule approximation to integrate density along the ray. This is not really accurate - the assumption leads to a blind average of transmission. Instead, integration was extended into a geometric product integral which approximates visibility as a summative integral exponent. Using a basic, branchless application of simpson's rule, a more apt transmission is achieved. It was discovered that the typical edge cases of simpson's rule do not apply in this case. Notably, there is no strict sampling requirement. Consider that a function of irradiance with ray depth will start at zero and end at zero (once the ray exits the volume). It happens that simpson's rule will be stable regardless of sample count. This is because the quadrature can 'substitute' zero terms to pad up to the requirement as the overall function starts and ends at zero. Therefore, a branchless simpson's rule is possible within shader.

Spectral rendering? Impossible!

A spectral approximation was developed, leveraging the Ångström exponent to 'compress' colour variance into a single optimised computation. This is possible by considering irradiance within CIE colourspace and utilising a single wavelet analytical colour matching function (CMF) to understand the distribution of irradiance across wavelengths. With a weight per wavelength, it is possible to apply the Ångström exponent before merging colour information as a single RGB value. The CMF is a standard gaussian form - well approximated using a Hermite-Gauss quadrature. Only four terms are required per wavelet for great accuracy. The CMF splits into four wavelets for three colour components (two for the red channel). Therefore, a 4x4 matrix of 16 wavelengths is adequate for basic spectral rendering of this form. Results of this work indicate spectral rendering only incurs a 3x performance penalty for these 16 wavelengths when utilising matrix and vector operations.

The haboob is of the ground, not the sky!

Scene integration of the haboob is more involved than other effects. After all, the haboob is present in the scene unlike screen covering or sky orientated effects.

Permutations of visibility

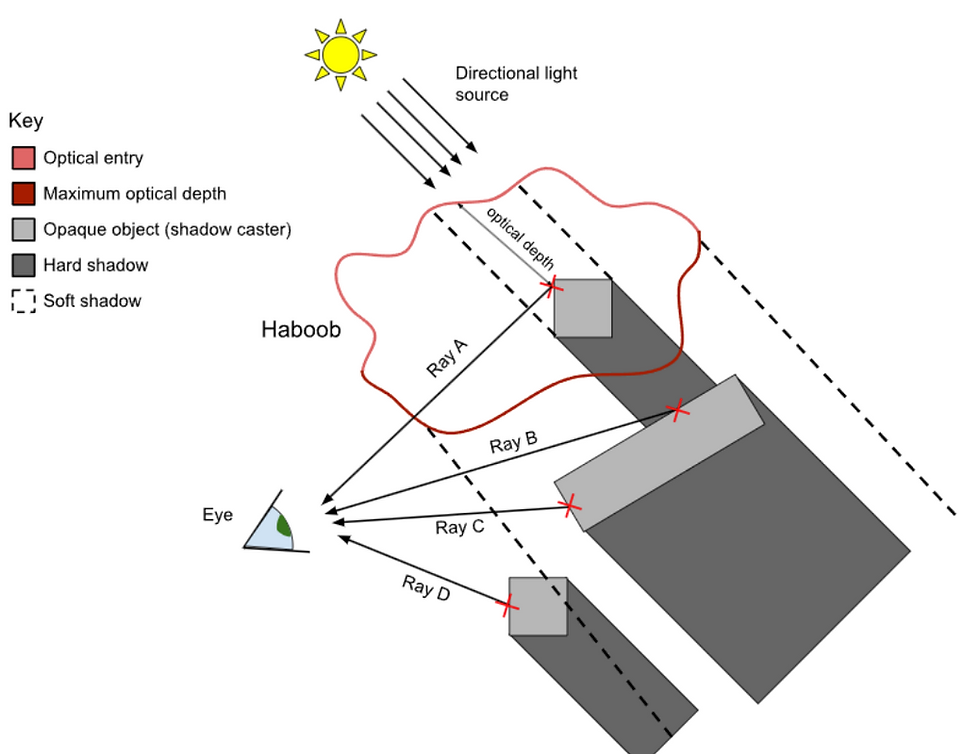
To decouple the scattering contributions from the volumetric pass, the Beer Shadow Map idea of Sébastien Hillaire was utilised - coupled with general exponential shadowmapping. The original BSM represents optical thickness as an average with geometric depth - which is not ideal. Consider that Beer-Lambert transmission exhibits an exponential falloff - any overapproximation of density has great bias. Also, the minimum and maximum extents used by the BSM are arbitrary. Any minor change in threshold will have a drastic effect on Ray A (in the diagram) due to a lack of distribution awareness. The employed solution to this problem was surprisingly subtle.

An assumption of density distribution

Assume the volume exhibits a gaussian distribution of density and any arbitrary threshold altering the extents has less influence on the outcome. Integrate this hypothetical distribution to discover a sigmoid-like function! Therefore, only the smoothstep blending function is necessary to improve the once linear blending BSM.

Luckily, this keeps the BSM to three channels. The fourth component was therefore used to include the integrated Ångström exponent within the BSM to achieve spectral shadowing. As the Ångström exponent has an unknown distribution, this value instead utilises the original linear blend.

Spectral shadowing

A stable, inversely proportional convergence...

Whilst the solution was discovered to rapidly converge towards a ground truth with sample count, the devised application is not perfect. It was discovered that even a two-term Henyey-Greenstein phase function with an ambient term will not adequately approximate scattering in the orthogonal directions to the light source. Therefore, haboob rendering critically requires a multiple scattering approximation.

Also, shadowing negatively affects the stability and convergence of irradiance integration. This is due to the high frequency binary information of the exponential shadow map and other complexities associated with sampling the BSM. The algorithm may be improved by using sub-samples or an independent trace all together for these maps.

Future food for thought.

After mulling over how to better space samples in a real-time context, a potential solution was discovered that appears to not be employed by literature. Unfortunately, this solution was discovered late within this study so only a generic rasterizer-supported constant spacing could be implemented. This may be investigated further as future work in general volumetric rendering.

Hopefully you enjoyed reading this blog post. This is my first ever blog post and I wish to find the time (and patience) to share more thoughts in the future!